Rubrica: Matematicamente, Speciale funzioni matematiche – 2
Titolo o argomento: Dominio Codominio Invertibilità Monotonia
Dominio
Con questo termine indichiamo la zona dell’asse x (ascisse) dove la funzione è presente. E ad esso sottraiamo la zona dell’asse delle x in cui la funzione non esiste. Detto in soldoni tramite il dominio sappiamo la porzione (il tratto – l’intervallo – la parte…) di asse delle x in cui la funzione passa sicuramente.
Codominio
Nel codominio vediamo fino a dove la funzione è presente sull’asse delle y (ordinate). Ad esempio, come vedremo nel prossimo articolo, le funzioni seno e coseno hanno codominio compreso tra -1 ed 1.
Può sembrarvi banale? Eppure durante diversi esami orali di Analisi Matematica 1 ho sentito molti, molti studenti non conoscere il dominio e il codominio della funzione tangente ad esempio… Per questo nel prossimo articolo trovate un interessante elenco.
Funzioni invertibili:
Una funzione è invertibile quando è sia iniettiva che suriettiva.
-
Iniettiva, in parole povere, significa che “distinti elementi di un insieme A, hanno distinte immagini nell’insieme B“. Tuttavia l’insieme B può avere anche altri elementi che non travano corrispondenza in A.
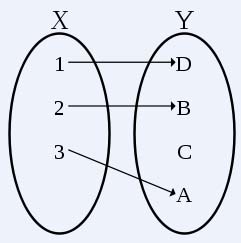
-
Suriettiva significa, sempre in termini semplificati, che “ogni elemento dell’insieme immagine B corrisponde ad un elemento dell’insieme A“. In soldoni non ci sono elementi liberi da legami…
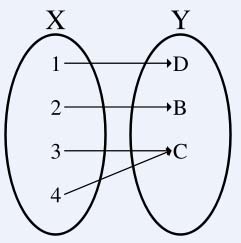
f(x) : A→B è la funzione diretta che va da A in B
f-1(x): B→A è la funzione inversa che va da B in A. Dominio e Codominio (immagine) semplicemente si scambiano.
Quando invertiamo una funzione esplichiamo la x e poi, per convenzione scambiamo le lettere… ovvero al posto della x mettiamo la y e viceversa:
funzione f(x) = y = 2x+1 esplichiamo la x e otteniamo x= (y-1)/2 scambiamo le lettere x,y e abbiamo y=(x-1)/2 che è la funzione inversa della funzione iniziale. Perchè si scambiano le lettere? Perchè il dominio diventa il codominio e viceversa…
Funzioni monotòne
Giusto per farvi capire il senso, una funzione monotòna è una funzione che non cambia comportamento ovvero una funzione crescente (ma potrebbe anche essere strettamente crescente) oppure una funzione decrescente (ma potrebbe essere strettamente decrescente). Non ditelo però al prof. con queste parole 🙂 Su qualunque libro di testo di Analisi matematica trovate (spero) un semplice paragrafo che esplica le condizioni di crescenza, decrescenza assai semplici.
Continua…
Link correlati
Speciale funzioni matematiche -1- Introduzione al concetto di funzione
Speciale funzioni matematiche -2- Dom Codom Invertibilità Monotonia
Speciale funzioni matematiche -3- Elenco funzioni matematiche note
Speciale funzioni matematiche -4- Come si studia una funzione
Speciale funzioni matematiche -5- Esercizio svolto in ogni sua parte

