Rubrica: Matematicamente
Titolo o argomento: Che cos’è il caos deterministico?
Una tra le più recenti scoperte della matematica sperimentale è il cosiddetto “caos deterministico”.
Quando un sistema dinamico (di qualsiasi natura e scala) è sufficientemente complesso e dotato di interazioni non lineari, la sua evoluzione nel tempo, nonostante sia governata da leggi rigorosamente “deterministiche”, può diventare “caotica”.
La soluzione degli algoritmi che descrivono l’evoluzione di un sistema dinamico prende il nome di “attrattore”. Il nome deriva dal fatto che la soluzione numerica dei sistemi di equazioni è normalmente di tipo iterativo, a “convergenza”. Tutto avviene in sostanza come se essa fosse dotata di un potere di “attrazione”, che appunto la attrae verso la convergenza.
Quando la curva rappresentativa dell’attrattore è “regolare”(un punto, un segmento, un cerchio, un ellisse, una qualsiasi curva unica o periodicamente ripetitiva) si ha un attrattore “ordinario”.
Quando invece è “irregolare” (una curva infinitamente aggrovigliata, mai ripetitiva) si ha un attrattore “strano, cioè “caotico”. La curva infinitamente aggrovigliata che si ottiene è un “frattale”: una linea infinitamente lunga e mai ripetitiva ma contenuta in un’area o un volume (o un iper-spazio) di dimensioni finite.
Il termine “frattale” deriva dal fatto che simili curve infinitamente aggrovigliate su sé stesse, finiscono per assumere caratteristiche di “quasi” superfici, “quasi” volumi, ecc., assumendo così dimensioni non intere, frazionarie, “frattali” appunto.
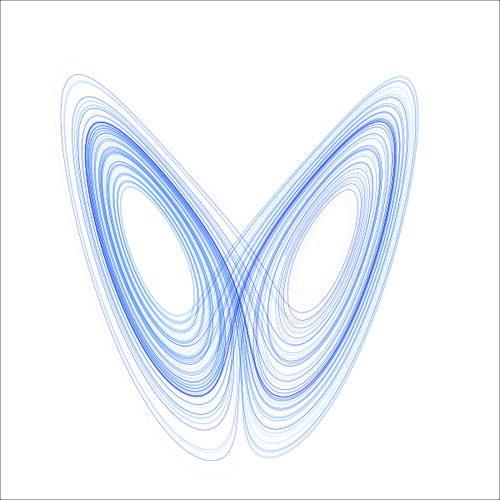
La più nota rappresentazione visiva di fenomeni caotici è la famosa “farfalla” di Edwin Lorenz la quale mostra l’evoluzione “caotica” del clima fornita da un modello meteorologico del 1963. L’attrattore di Lorenz esprime il noto concetto di “effetto farfalla” e cioè che in sistemi caotici, piccole differenze nelle condizioni iniziali possono originare, dopo un tempo sufficiente, grandi differenze nelle condizioni finali.
Il caos deterministico è stato perciò impropriamente anche definito come la possibilità che “piccole cause possano generare grandi effetti”. In questo senso è diventato famoso l’aforisma di Lorenz secondo cui: ” il battito delle ali di una farfalla in Brasile, può provocare un uragano nel Texas”. In realtà in senso “fisico” è errato dire che “piccole cause possono generare grandi effetti”. E’ invece corretto affermare che un’infinità di microcause (ognuna di per sé trascurabile), agendo su tempi sufficientemente lunghi, possono produrre per accumulo macro effetti non trascurabili.