Rubrica: Officina della Matematica
Titolo o argomento: Gli assiomi del campo e dello spazio vettoriale
In tutti gli insiemi numerici studiati in geometria sono definite due operazioni: la somma (+) ed il prodotto (·). Questi godono delle proprietà riportate di seguito le quali prendono il nome di assiomi campo.
Assiomi campo
1. Proprietà associativa della somma: per ogni a, b, c si ha che (a + b) + c = a + (b + c).
2. Esistenza dell’elemento neutro per la somma: esiste un “a0” tale che per ogni “a” abbiamo che (a + a0) = (a0 + a) = a, dove l’elemento a0 (ovvero l’elemento neutro) non è altro che lo zero.
3. Esistenza dell’opposto: per ogni “a” esiste un “a1” tale che (a + a1) = (a1 + a) = a0, dove a1 non è altro che -a.
4. Proprietà commutativa della somma: per ogni a + b = b + a.
–
5. Proprietà distributiva della somma rispetto al prodotto: per ogni a, b, c si ha che a · (b + c) = a · b + a · c.
6. Proprietà associativa del prodotto: per ogni a, b, c si ha che (a · b) · c = a · (b · c).
7. Esistenza dell’elemento neutro per il prodotto: esiste un “a1” tale che per ogni a · a1 = a1 · a = a, dove l’elemento a1 (ovvero l’elemento neutro) non è altro che 1.
8. Esistenza dell’inverso: per ogni a diverso da zero, esiste un ã tale che a · ã = ã · a = a1, dove l’elemento “a1″ non è altro che a-1 ovvero 1/a.
9. Proprietà commutativa del prodotto: per ogni a, b si ha che a · b = b · a
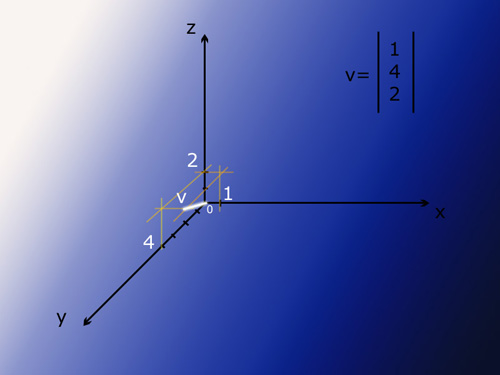
Uno spazio vettoriale (ovvero uno spazio lineare) su R (l’insieme dei Reali) è un insieme che possiamo chiamare V dove sono definite due operazioni: la somma (dove due elementi di V, sommati, formano un nuovo elemento di V) ed il prodotto per scalari (dove il prodotto di un elemento di R per uno di V, mi restituisce un elemento di V). La somma ed il prodotto per scalari soddisfano le proprietà riportate di seguito le quali prendono il nome di assiomi dello spazio vettoriale.
Note
Gruppo: trattasi di un insieme che soddisfa le proprietà 1, 2, 3 sopra elencate
Gruppo commutativo: un insieme che soddisfa le proprietà 1, 2, 3, 4 sopra elencate
Anello: si tratta di un insieme che soddisfa le proprietà 1, 2, 3, 4, 5, 6, 7 sopra elencate
Anello commutativo: un insieme che soddisfa le proprietà 1, 2, 3, 4, 5, 6, 7, 9 sopra elencate
Corpo: un insieme che soddisfa le proprietà 1, 2, 3, 4, 5, 6, 7, 8 sopra elencate
Campo: un insieme che soddisfa tutte le proprietà 1-9 sopra riportate
Assiomi spazio vettoriale
1. Per ogni u, v, w appartenenti allo spazio vettoriale V, si ha che: (u + v) + w = u + (v + w).
2. Esiste uno 0 appartenente allo spazio vettoriale V tale che, per ogni elemento v appartenente a V, si ha che: v + 0 = 0 + v = v.
3. Per ogni elemento v appartenente allo spazio vettoriale V, esiste un elemento -v (sempre appartenente allo spazio vettoriale V) tale che: v + (-v) = (-v) + v = 0.
4. Per ogni v, w appartenenti allo spazio vettoriale V si ha che: v + w = w + v.
–
5. Per ogni λ appartenente ad R (l’insieme dei Reali) e per ogni v, w appartenenti allo spazio vettoriale V si ha che: λ · (v + w) = λ · v + λ · w.
6. Per ogni λ, μ appartenenti ad R (l’insieme dei Reali) e per ogni v appartenente allo spazio vettoriale V si ha che: (λ + μ) · v = λ · v + μ · v.
7. Per ogni λ, μ appartenenti ad R (l’insieme dei Reali) e per ogni v appartenente allo spazio vettoriale V si ha che: (λ · μ) · v = λ · (μ · v).
8. Per ogni elemento v appartenente allo spazio vettoriale V si ha che: 1 · v = v e 0 · v = 0.