Rubrica: Energia
Titolo o argomento: Dalla deformazione alla corrente e viceversa
Vi sono dei cristalli solidi i quali, se sottoposti ad una sollecitazione meccanica di compressione o di torsione, generano una differenza di potenziale tra le loro superfici. Affinché ciò sia possibile essi devono necessariamente essere tagliati in sottili lamine secondo un preciso asse. Come per la termoelettricità (vedi l’articolo: Che cos’è la termoelettricità?) si tratta di un “effetto reversibile” che si manifesta su scala nanometrica. I cristalli piezoelettrici di rilevante interesse sono il quarzo (caratterizzato da ottima resistenza agli urti ed al calore), la tormalina (inattaccabile dagli acidi) ed il sale di Seignette o sale di Rochelle (presenta un’altissima piezoelettricità). Si tratta di minerali appartenenti a classi di simmetria con assi polari. L’effetto, che è stato scoperto ad opera dei fratelli Curie nel 1880, può essere distinto tra “diretto” (o primario), “inverso” (o reciproco – scoperto in seguito da Lippman), “longitudinale” e “trasversale”.
Effetti
L’effetto diretto consiste nella polarizzazione elettrica prodotta nelle due facce del cristallo da uno sforzo meccanico; tale polarizzazione cambia di segno con l’inversione dello sforzo. L’effetto inverso, invece, in seguito all’applicazione di un campo elettrico, produce una deformazione meccanica. Si ha l’effetto longitudinale qualora una dilatazione in una data direzione produce una polarizzazione nella medesima direzione. Infine, qualora si verifichi una dilatazione perpendicolare al campo elettrico che la produce, ci troviamo davanti all’effetto trasversale. Affinché un cristallo sia ritenuto piezoelettrico, deve necessariamente essere caratterizzato dall’effetto primario e da quello inverso.
Assi
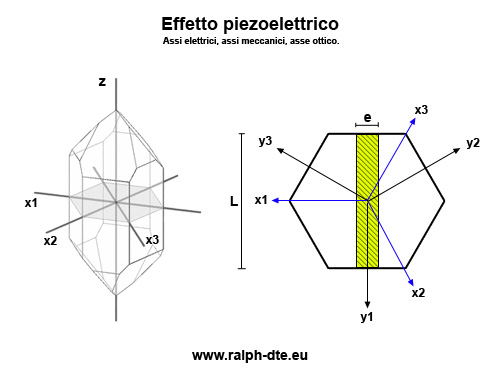
Un cristallo piezoelettrico, ad esempio il quarzo, è caratterizzato dai seguenti assi: l’asse ottico (rappresentato in figura dall’asse z) il quale altro non è che l’asse di simmetria del cristallo, gli assi elettrici (rappresentati in figura con x1, x2, x3) i quali congiungono i vertici opposti dell’esagono su un piano perpendicolare all’asse z e gli assi meccanici (rappresentati in figura con y1, y2, y3) i quali congiungono i punti medi dei lati dell’esagono.
L’esperimento di Curie
Curie tagliò un cristallo di quarzo ricavandone una lamina parallelepipeda (la sezione rettangolare è marcata dalla zona gialla in figura) di lati “L” x “e” x “d” paralleli rispettivamente a un asse meccanico, a un asse elettrico ed all’asse ottico. Egli riscontrò quanto segue:
Applicando una forza meccanica F lungo la direzione dell’asse elettrico, sulle facce perpendicolari a tale asse si maniferstano due cariche opposte (q1 e -q1) legate alla forza mediante la relazione: q1 = k·F, dove k è una costante.
Applicando una forza F lungo l’asse meccanico (direzione perpendicolare alla precedente), sulle stesse facce del caso precedente, cioè sulle facce perpendicolari all’asse elettrico, si manifestano due cariche opposte (q2 e -q2) legate alla forza mediante la relazione: q2 = -k·L/e·F, dove k è la stessa costante mensionata precedentemente, “L” ed “e” sono le dimensioni della sezione del parallelepipedo ed F è la forza applicata.
Applicando una forza F lungo l’asse ottico non si produce alcun effetto di polarizzazione.
Applicando una differenza di potenziale V tra le facce perpendicolari all’asse elettrico, e quindi polarizzando elettricamente la sbarretta, si produce una dilatazione (o una contrazione) S, in direzone dello stesso asse, proporzionale a V secondo la relazione: S = k’·V (effetto longitudinale).
Applicando la medesima differenza di potenziale V del caso precedente tra le medesime facce perpendicolari all’asse elettrico, si produce anche una dilatazione (o contrazione) S’ lungo l’asse meccanico secondo la relazione: S’ = -k’·L/e·V (effetto trasversale).
Vibrazione forzata e risonanza
L’effetto inverso è stato largamente sfruttato per numerosi impieghi. Applicando infatti una corrente alternata alle facce di una lamina piezoelettrica si produce una vibrazione forzata di ampiezza notevolmente ridotta. Quando i valori della frequenza sono prossimi a quelli della frequenza della lamina si raggiunge il fenomeno della risonanza il quale permette di ottenere oscillazioni di ampiezza assai elevata. Il fenomeno della risonanza ha permesso di utilizzare la piezoelettricità per numerose applicazioni altrimenti non realizzabili con comuni circuiti.
Applicazioni
Risonatori al quarzo generanti onde acustiche (Paul Langevin) ovvero i sonar; interferometri acustici per la misura della velocità del suono; applicazioni radiotecniche; attuatori; trasduttori di pressione; accelerometri; sensori (largamente utilizzati per la telemetria dei veicoli e motoveicoli da corsa); motori lineari e rotativi piezoelettrici; sensori ed attuatori modali per il controllo delle vibrazioni di strutture; sensori ed attuatori modali per il controllo del rumore irradiato; microfoni piezoelettrici; microfoni a pressione; microfoni a cellula; microfoni unidirezionali; altoparlanti piezoelettrici; cuffie piezoelettriche; apparecchiature medicali…