Rubrica: Matematicamente, Speciale funzioni matematiche – 3
Titolo o argomento: Funzioni matematiche note (un rapido elenco)
Un elenco apparentemente lungo… …in realtà sintetico, per sapere le generalità in modo veloce
Andando un pò più nello specifico rispetto al precedente articolo sulle funzioni matematiche desidero elencarvi e illustrarvi le più comuni funzioni note. Questo perchè ho notato come durante gli esami orali, studenti che hanno preso ottimi voti allo scritto, non sanno bene come rappresentarle su un foglio e soprattutto non ne conoscono il dominio e il codominio… Fatto strano ma che accade spesso.
Legenda: Indicherò con D il dominio della funzione, con C il codominio e con I l’intervallo di invertibilità della funzione. Mi raccomando, abituatevi al pensiero di cosa vogliano dire i suddetti termini anche perchè ogni testo che trovate adotta diverse lettere per rappresentarli e così ogni sito, forum ecc… Se non imparate a memoria ma ne conoscete il significato non incontrerete problemi insormontabili.
Funzioni lineari
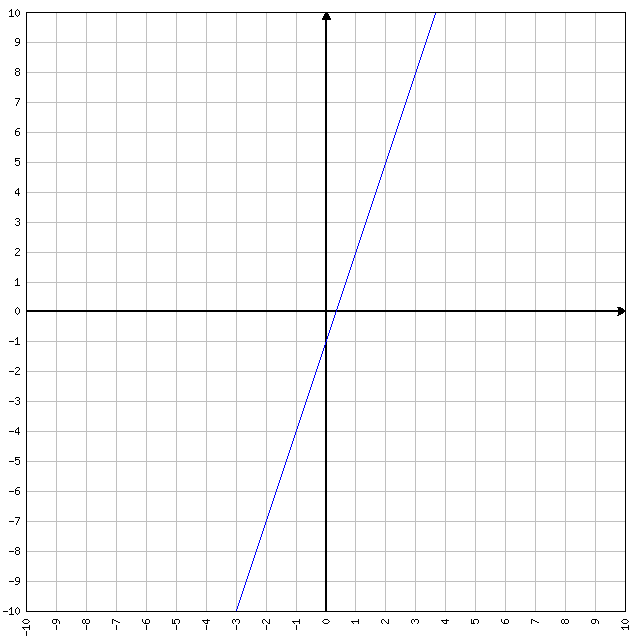
Un esempio semplice y=3x-1 ma potrebbe essere una qualunque altra funzione nella forma y=mx+q. Quando dobbiamo descrivere un asintoto obliquo in uno studio di funzione si ricorre ad una funzione lineare.
Funzione valore assoluto (modulo)
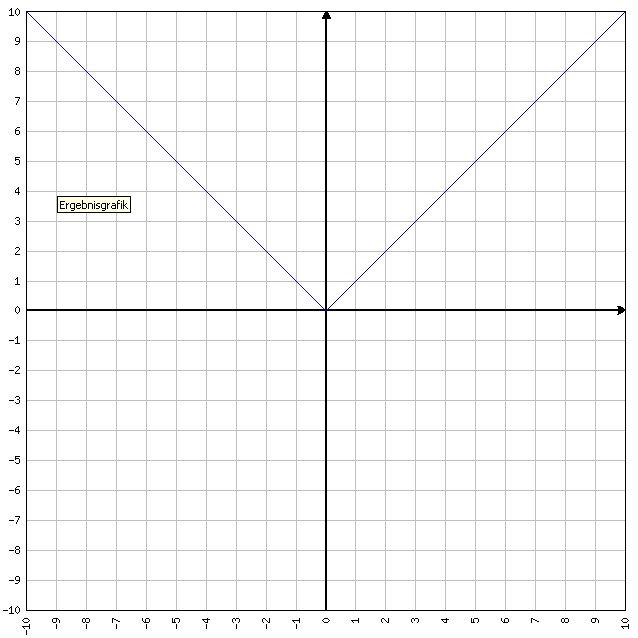
Un esempio y=|x| che è y=x se x≥0 oppure y=-x se x ≤0 esattamente come si vede nell’immagine sopra. In una qualunque funzione contenente il modulo(vedremo in seguito), si vede dove questo si azzera e poi si definisce l’argomento positivo oltre il punto in cui si azzera e negativo prima dello stesso punto. Se vi è più di un modulo, il metodo di risoluzione diventa molto simile a quello delle disequazioni… ma lo vedremo nello specifico in seguito.
y=|x|
-
Dominio uguale a tutto l’insieme dei Numeri Reali D=R
-
Codominio contenuto tra zero e più infinito C= [0,+∞)
-
Invertibilità tra zero e più infinito I=[0,+∞)
Funzione seno
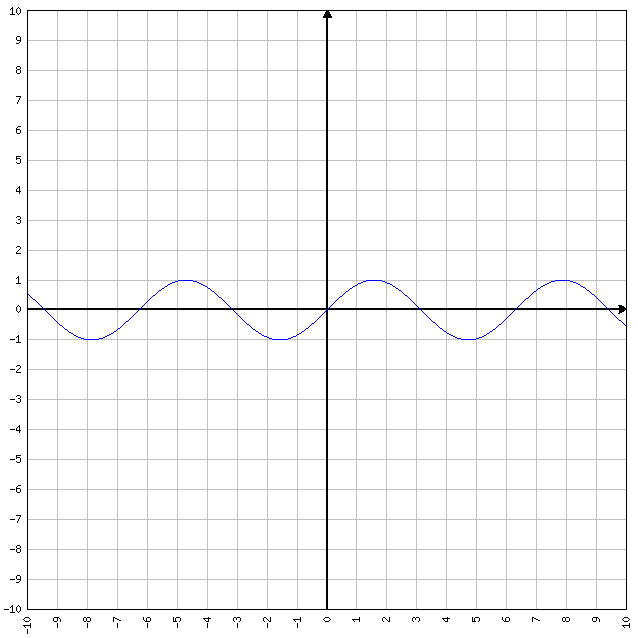
y = sin x
-
D=R
-
C=[-1,1]
-
I=[-π/2, π/2]
-
potete ricordarvi che il seno di zero vale zero come vedete nell’immagine sopra, per ricordarvi come disegnarla e per non fare confusione con il coseno.
Funzione coseno
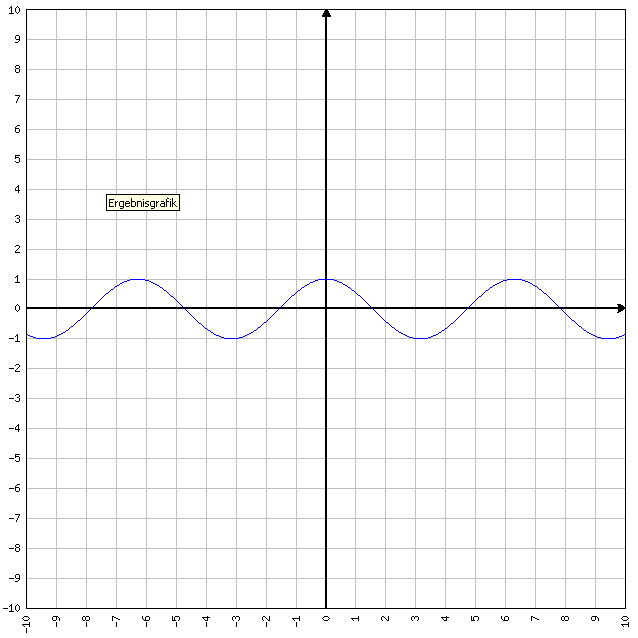
y = cos x
- D=R
- C=[-1,1]
- I=[0, π]
Funzione tangente
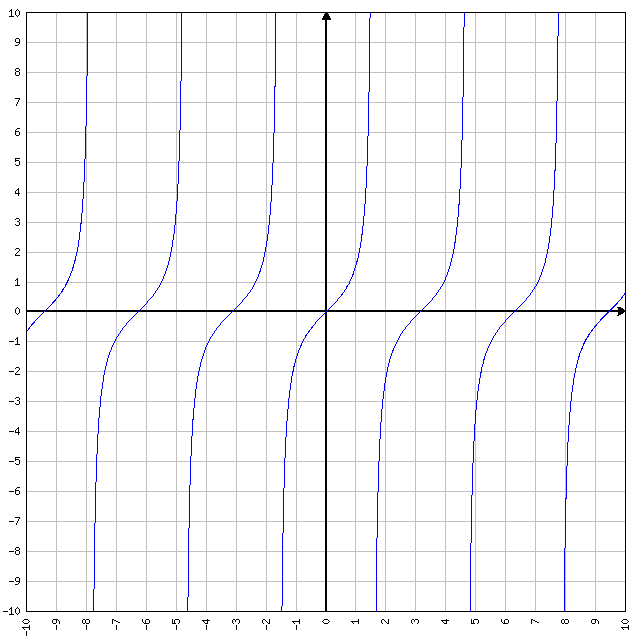
y = tg x
- D=R-[π/2+kπ]
- C=R
- I=(-π/2, π/2)
- Può essere interessante notare che la tangente, essendo uguale al seno fratto il coseno, non esiste quando il coseno vale zero. Ovviamente.
Funzione potenza

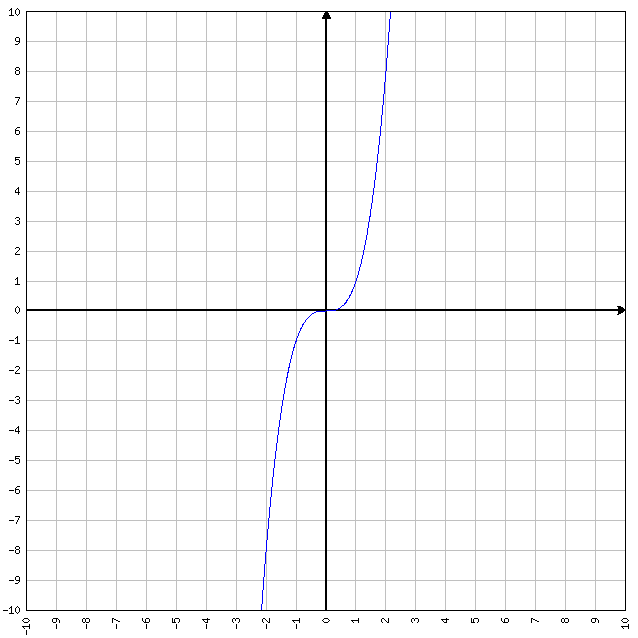
y = xn
Nell’immagine sopra a sinistra abbiamo y = x2
-
D=R
-
C=[0, +∞)
-
I= [0, +∞)
Mentre in quella a destra abbiamo y = x3
-
D=R
-
C=R
-
I=R
Funzione esponenziale
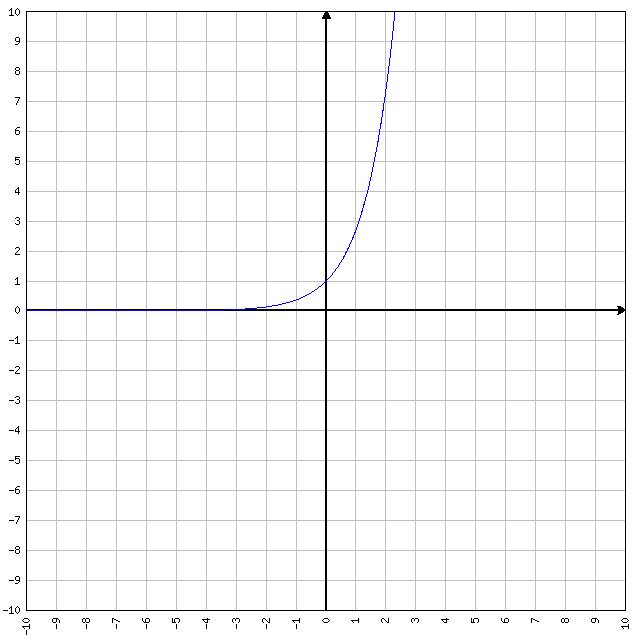
y = ax
- D=R
- C=(0, +∞)
- I=R
Funzione logaritmo
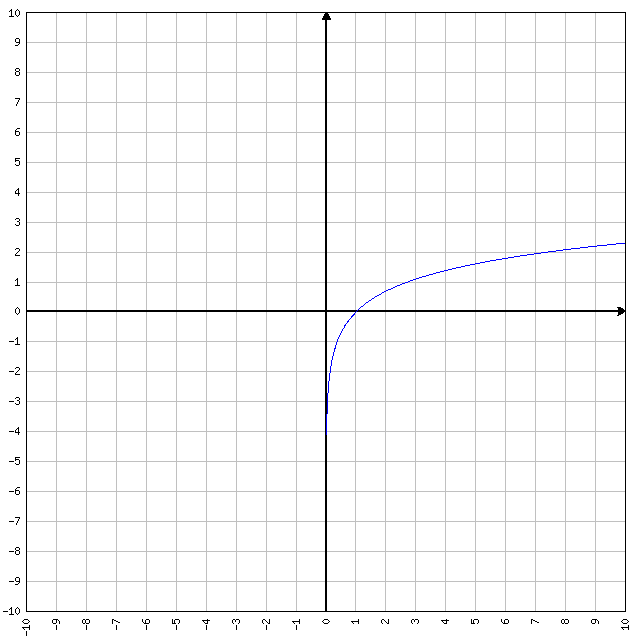
y = logax
- D=(0, +∞)
- C=R
- I=(0, +∞)
Funzione arcotangente
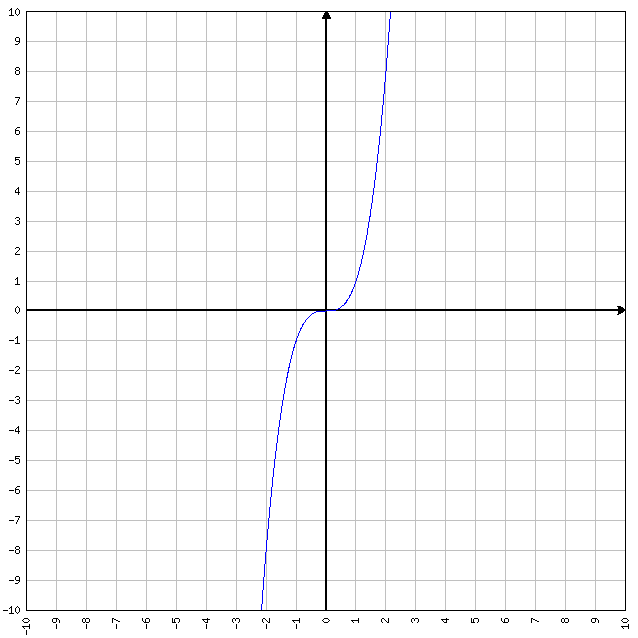
y = arctg x
- D=R
- C=(-π/2, π/2)
- I=R
- Si tratta della funzione inversa della tangente ossia tan-1x
Funzione arcoseno
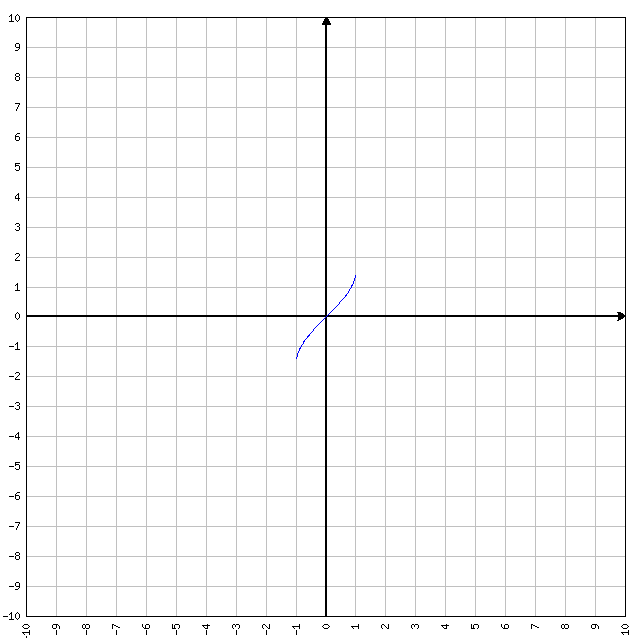
y = arcsen x
- D=[-1, 1]
- C=[-π/2, π/2]
- I=[-1, 1]
- Funzione inversa del seno
Funzione arcocoseno
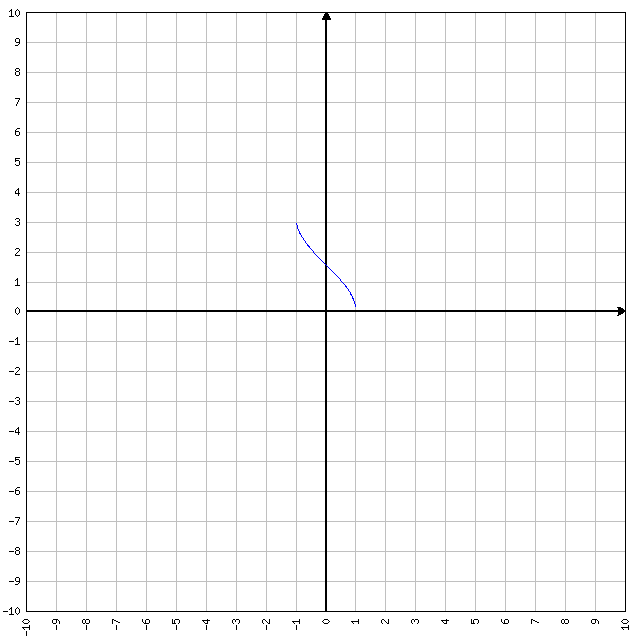
y = coseno x
- D=[-1, 1]
- C=[0, π]
- I=[-1, 1]
- Funzione inversa del coseno
Funzione cotangente
Potete provare a ricavare voi i dati sapendo che la tangente è data dal rapporto tra il seno diviso il coseno, mentre la cotangente è il reciproco ossia è data dal rapporto tra il coseno diviso il seno.
Funzione arcocotangente
Potete provare a ricavare voi i dati sapendo che l’arcocotangente è la funzione inversa della cotangente.
Funzioni iperboliche
Seno iperbolico
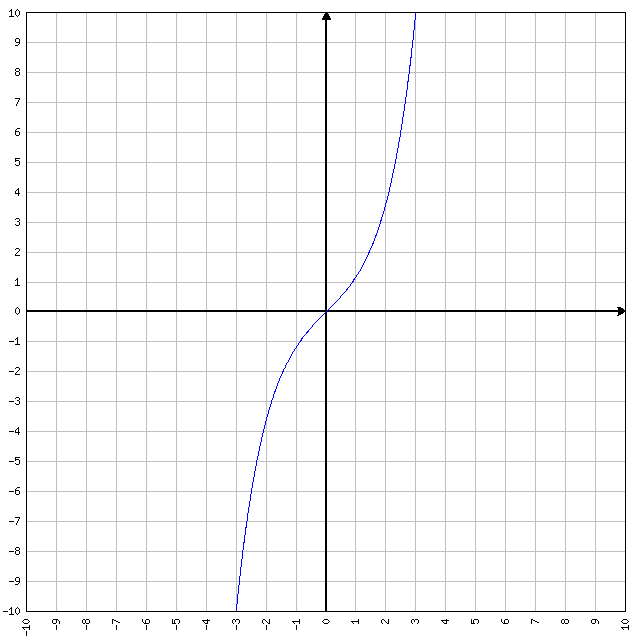
y = senh x
- D=R
- C=R
- I=R
- la sua funzione inversa è la funzione settore seno iperbolico
Coseno iperbolico
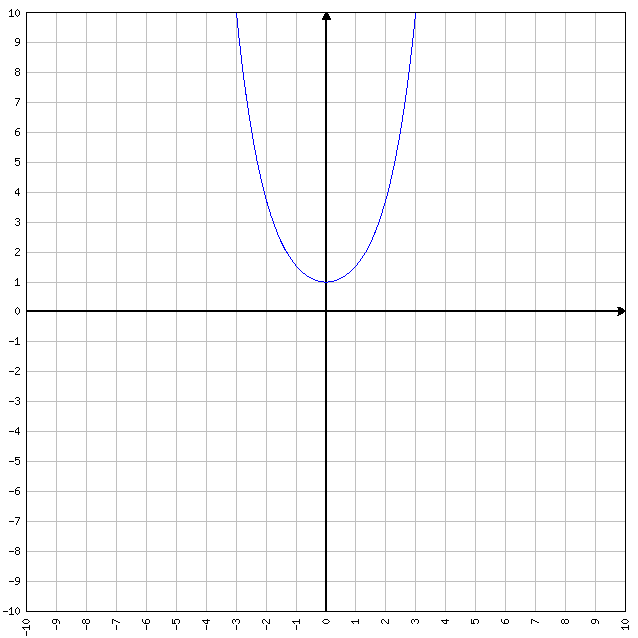
y = cosh x
- D=R
- C=[1, +∞)
- I= Non è invertibile su R. Nota però che il coseno iperbolico, come applicazione da [0,+∞) in [1,+∞) è invertibile
- la sua funzione inversa è la funzione settore coseno iperbolico
Tangente iperbolica
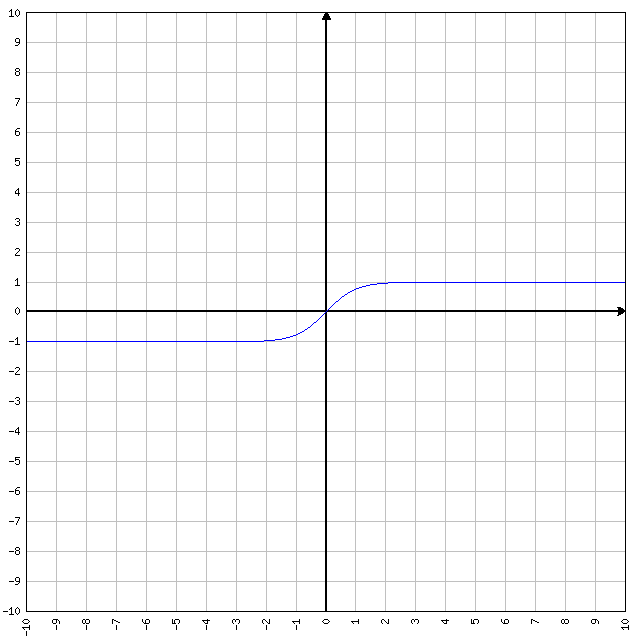
y = tanh x
- D=R
- C=(-1,1)
- I=R
- la sua funzione inversa è la funzione settore tangente iperbolica
e ancora:
y=1/x
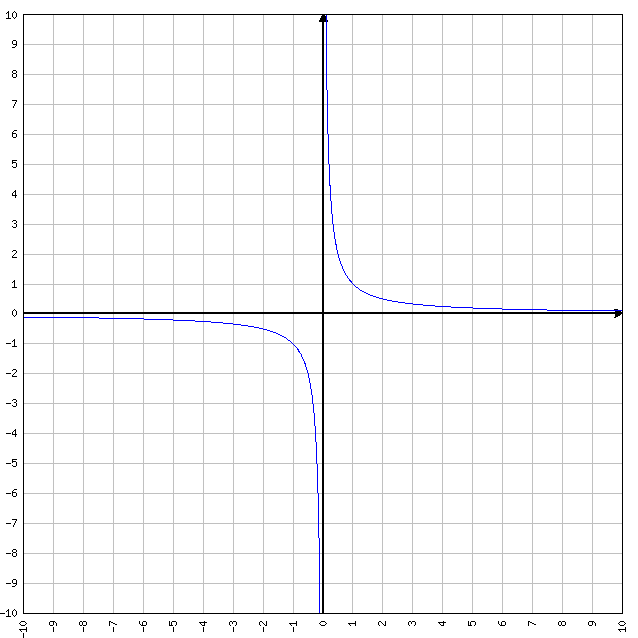
- D=R-[0]
- C=R-[0]
- I=R-[0]
y=√x
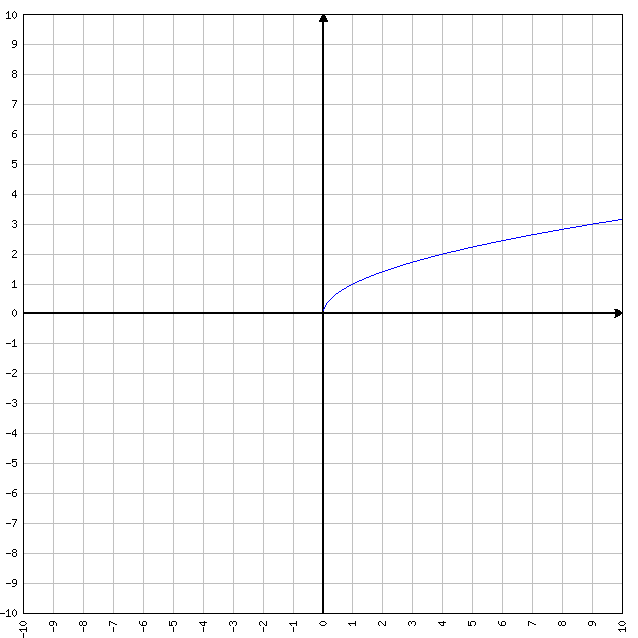
- D=[0, +∞)
- C=[0, +∞)
- I=[0, +∞)
Continua…
Utilità
Link correlati
Speciale funzioni matematiche -1- Introduzione al concetto di funzione
Speciale funzioni matematiche -2- Dom Codom Invertibilità Monotonia
Speciale funzioni matematiche -3- Elenco funzioni matematiche note
Speciale funzioni matematiche -4- Come si studia una funzione
Speciale funzioni matematiche -5- Esercizio svolto in ogni sua parte

